---

Você sabe o que é estática na Física?

Neste artigo, vamos abordar os princípios da estática na mecânica, destacando a diferenciação entre equilíbrio estático e dinâmico, dois conceitos fundamentais que desempenham um importante papel no estudo do comportamento dos objetos em repouso e das forças que atuam sobre eles.

---

Introdução aos conceitos de estática

A estática ao contrário da dinâmica, que lida com movimentos e acelerações se concentra nas situações em que as forças estão em equilíbrio.

Esse conteúdo é parte integrante da Mecânica, que é a área da física que estuda o movimento e o equilíbrio dos corpos. Ela fornece a base teórica e os princípios essenciais para a análise de estruturas e sistemas mecânicos, desde pequenos componentes até grandes construções.

O principal objetivo da Estática é determinar as condições sob as quais um objeto ou sistema está em equilíbrio estático, ou seja, não apresenta movimento ou rotação acelerados. Para isso, são consideradas as forças que atuam sobre o objeto, bem como os momentos resultantes dessas forças.

Para analisar e resolver problemas estáticos, é comum utilizar diagramas de corpo livre, que representam todas as forças atuantes sobre um objeto de interesse. Além disso, a aplicação dos princípios da Estática requer conhecimento sobre vetores, pois as forças e momentos são grandezas vetoriais que possuem magnitude, direção e sentido.

Ao compreender os princípios fundamentais da Estática, torna-se possível realizar análises precisas e tomar decisões adequadas em relação ao equilíbrio de sistemas.

Princípios Fundamentais da Estática

No estudo da Estática, existem princípios fundamentais que são essenciais para a compreensão e análise do equilíbrio de corpos e sistemas.

Esses princípios estabelecem as condições necessárias e suficientes para que um objeto esteja em equilíbrio estático. Vamos explorar alguns desses princípios:

1. Equilíbrio Estático: O equilíbrio estático ocorre quando as forças e os momentos que atuam sobre um corpo estão balanceados, resultando em ausência de movimento ou rotação acelerados. Para que um objeto esteja em equilíbrio estático, duas condições devem ser atendidas:
   • A soma vetorial de todas as forças que atuam no corpo deve ser igual a zero.
   • A soma vetorial de todos os momentos (ou torques) resultantes dessas forças em relação a qualquer ponto também deve ser igual a zero.
2. Forças e Momentos: Na Estática, as forças são representadas como vetores, que possuem magnitude, direção e sentido. Elas podem ser aplicadas em diferentes pontos de um corpo, resultando em momentos, também conhecidos como torques. Um momento é o produto da força pela distância perpendicular entre o ponto de aplicação da força e o ponto de referência.
3. Diagramas de Corpo Livre: Os diagramas de corpo livre são ferramentas essenciais na análise estática. Eles consistem na representação gráfica de um objeto isolado, mostrando todas as forças que atuam sobre ele, incluindo as forças externas e as reações nos pontos de apoio. Esses diagramas permitem visualizar claramente as forças envolvidas e facilitam a determinação das forças resultantes e dos momentos.
4. Princípio da Transmissibilidade das Forças: O princípio da transmissibilidade das forças estabelece que uma força pode ser considerada a mesma, independentemente de onde é aplicada ao longo de sua linha de ação. Em outras palavras, a força resultante em um objeto é a mesma, independentemente de seu ponto de aplicação. Esse princípio é útil para simplificar a análise de sistemas complexos, reduzindo múltiplas forças aplicadas a uma única força resultante.

Ao aplicar esses princípios fundamentais da Estática, é possível determinar as forças e momentos envolvidos em um sistema e verificar se ele está em equilíbrio estático.

Esses princípios são a base para a resolução de problemas estáticos em diversas áreas, desde engenharia civil e mecânica até arquitetura e biomecânica. Ao compreender e aplicar esses conceitos, os engenheiros e cientistas podem projetar estruturas seguras e eficientes, garantindo a estabilidade e o bom funcionamento de sistemas em equilíbrio.

Estática do ponto material

A estática do ponto material é um ramo da Física que se concentra no estudo do equilíbrio de um objeto ou partícula, considerando-o como um ponto material, ou seja, desconsiderando suas dimensões físicas e considerando apenas sua massa e posição no espaço.

Nesse contexto, um ponto material é tratado como uma partícula que não possui dimensões físicas significativas, sendo representado por sua massa concentrada em um único ponto.

Essa simplificação permite uma análise mais simples e direta, especialmente quando as dimensões do objeto não são relevantes para o problema em questão.

A estática do ponto material envolve a aplicação dos princípios fundamentais da Estática, como o equilíbrio de forças e o equilíbrio de momentos.

Para que um ponto material esteja em equilíbrio estático, é necessário que a soma das forças atuantes sobre ele seja igual a zero e que a soma dos momentos em relação a qualquer ponto seja igual a zero.

A análise da estática do ponto material é frequentemente aplicada em problemas que envolvem sistemas simples, como a análise de forças em uma partícula em repouso ou em movimento constante.

Exemplo:

1. (UNI-RIO) O corpo M representado na figura pesa e é mantido em equilíbrio por meio da corda AB e pela ação da força horizontal  de módulo . Considerando , a intensidade da tração na corda AB, suposta ideal, em N, é:

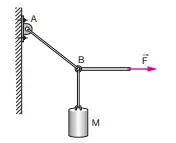
vamos fazer um diagrama de forças para que o corpo esteja em equilíbrio, tomando como base o ponto B.

Para que esteja em equilíbrio, a somatória das forças deve ser igual a zero, não há torques no problema.

Logo, a componente vertical da tração deve ser igual ao peso e a componente horizontal deve ser igual a força. Dessa forma podemos somar vetorialmente as componente para achar o valor da tração. Usando Pitágoras temos:

   

   

Estática do corpo extenso

Ao contrário da estática do ponto material, em que as dimensões do objeto são negligenciadas, a estática do corpo extenso leva em conta a geometria, a massa e a distribuição de massa do corpo para determinar as condições de equilíbrio.

A análise da estática do corpo extenso envolve a aplicação dos princípios fundamentais da Estática, como o equilíbrio de forças e o equilíbrio de momentos.

Para que um corpo extenso esteja em equilíbrio estático, é necessário que a soma vetorial das forças atuantes sobre ele seja igual a zero e que a soma vetorial dos momentos resultantes seja igual a zero.

Além disso, a estática do corpo extenso também considera a resolução de problemas envolvendo momentos de inércia, que são grandezas relacionadas à distribuição de massa do corpo em relação a um eixo de rotação.

Os momentos de inércia influenciam a resistência do corpo à rotação e são essenciais na análise de equilíbrio de corpos extensos que estão sujeitos a momentos de torque.

Para analisar a estática do corpo extenso, é comum utilizar diagramas de corpo livre, onde todas as forças externas e as reações nos apoios são representadas.

A partir desses diagramas, podem ser determinadas as condições de equilíbrio, bem como a relação entre as forças e os momentos envolvidos.

A estática do corpo extenso é amplamente aplicada em áreas como engenharia civil, mecânica, arquitetura e outras disciplinas relacionadas.

Ela permite a análise e o projeto de estruturas complexas, como pontes, edifícios, máquinas e sistemas mecânicos, levando em consideração a geometria, a massa e a distribuição de massa desses corpos para garantir sua estabilidade e segurança.

Momentos e Equilíbrio de Momentos

1. Vetores Momento: O momento, também conhecido como torque, é uma grandeza vetorial que descreve a tendência de rotação de um objeto em torno de um ponto específico. O momento é o produto vetorial do vetor força pela distância perpendicular entre o ponto de referência e a linha de ação da força. O momento é medido em unidades de força vezes distância (exemplo: newton-metro ou libra-pé).
2. Braço de Momento e Ponto de Referência: O braço de momento é a distância perpendicular entre o ponto de referência escolhido e a linha de ação da força. É importante selecionar um ponto de referência adequado para a análise do momento, pois a escolha do ponto influencia o valor do momento resultante. Geralmente, escolhe-se um ponto que facilite os cálculos ou que seja conveniente para a análise do sistema em questão.
3. Equilíbrio de Momentos em Relação a um Ponto: Para que um objeto esteja em equilíbrio estático, além do equilíbrio das forças, é necessário que o equilíbrio de momentos seja alcançado. Isso significa que a soma dos momentos resultantes das forças em relação a um ponto de referência escolhido deve ser igual a zero. Essa condição pode ser expressa pela equação: ΣM = 0, em que ΣM representa a soma dos momentos e deve ser igual a zero para que haja equilíbrio.
4. Momento Resultante e Equilíbrio de Momentos em Relação a um Eixo: Além do equilíbrio de momentos em relação a um ponto, também é possível analisar o equilíbrio de momentos em relação a um eixo. Nesse caso, o momento resultante é calculado como a soma dos momentos resultantes das forças em relação ao eixo escolhido. Assim como no equilíbrio em relação a um ponto, a condição para o equilíbrio de momentos em relação a um eixo é que a soma dos momentos resultantes seja igual a zero.

Exemplos Práticos e Estudos de Caso

Aqui estão alguns exemplos práticos e estudos de caso que ilustram a aplicação da estática em situações reais:

1. Pontes Suspensas: As pontes suspensas são estruturas complexas que exigem uma análise cuidadosa da estática para garantir sua estabilidade. O projeto e a construção de uma ponte suspensa envolvem a consideração de forças, momentos e equilíbrio estático. Estudos de caso, como a Ponte Golden Gate em San Francisco, Califórnia, ou a Ponte Akashi Kaikyō no Japão, destacam a aplicação dos princípios da estática para garantir que a estrutura seja capaz de suportar as forças externas e permanecer em equilíbrio.
2. Arranha-céus: A construção de arranha-céus também requer uma análise precisa da estática para garantir sua estabilidade. A consideração das cargas verticais, como o peso próprio do edifício e as cargas impostas pelos usuários, é fundamental. Além disso, a análise das forças horizontais, como o vento e os terremotos, é essencial para garantir que o arranha-céu seja capaz de resistir a essas solicitações. Estudos de caso de arranha-céus famosos, como o Burj Khalifa em Dubai ou o One World Trade Center em Nova York, ilustram a aplicação da estática na concepção e construção dessas estruturas impressionantes.

3. Engenharia de Pontos de Apoio: A estática desempenha um papel crucial no projeto de pontos de apoio, como roldanas, engrenagens e articulações. Esses elementos são fundamentais em mecanismos, máquinas e sistemas que envolvem movimento. A análise da estática é essencial para garantir que as forças e momentos sejam adequadamente distribuídos nos pontos de apoio, evitando falhas ou desgastes prematuros. Exemplos práticos incluem sistemas de engrenagens em máquinas industriais e pontos de apoio em veículos automotores.
4. Estabilidade de Estruturas Geotécnicas: A estática também é aplicada na estabilidade de estruturas geotécnicas, como taludes, barragens e muros de contenção. A análise da estática é utilizada para determinar as forças e momentos resultantes no solo e nas estruturas, garantindo a estabilidade dessas construções. Estudos de caso de barragens, como a Barragem de Itaipu na fronteira entre Brasil e Paraguai, ou de taludes de escavação em projetos de construção civil, ilustram a importância da estática na engenharia geotécnica.

Para mais busque aqui.