Entenda o que é um lançamento vertical e como podemos utilizá-lo.
Neste artigo, vamos explorar a Física por trás do lançamento vertical, compreendendo o seu funcionamento e os princípios que o regem ao lançar objetos diretamente para cima.
O lançamento vertical na Física é um conceito fundamental para compreender a trajetória de um objeto lançado para cima, sujeito apenas à força da gravidade.
Esse fenômeno, presente em situações cotidianas e vital na astronáutica, nos leva a explorar as leis do movimento e da gravidade que o governam.
SAIBA+ 10 Experimentos de Física que você pode fazer
Lançamento Vertical: O que é e como funciona?

Lançamento vertical, ou lançamento vertical, é um método de lançamento de foguetes e outras naves espaciais verticalmente no espaço. Este método é comumente usado por agências espaciais e empresas privadas para lançar satélites, sondas e outras espaçonaves em órbita.
O lançamento vertical é um processo complexo que requer precisão e planejamento cuidadoso para garantir um lançamento bem-sucedido. Ele envolve vários estágios, incluindo a ignição dos motores do foguete, a liberação dos grampos de lançamento e a ascensão do foguete ao espaço.
O foguete deve ser projetado para suportar as forças e temperaturas extremas que encontrará durante o lançamento, e o local de lançamento deve ser escolhido com cuidado para garantir que o foguete possa ascender com segurança ao espaço sem colocar pessoas ou propriedades no solo em perigo.
Esse estudo tornou-se um método cada vez mais importante de lançamento de espaçonaves, pois permite maior flexibilidade e precisão no lançamento de cargas em órbita. Também permite que espaçonaves sejam lançadas de uma ampla variedade de locais, incluindo áreas remotas ou inóspitas. À medida que a exploração espacial continua avançando, o lançamento vertical provavelmente continuará sendo um componente crítico da tecnologia de lançamento espacial.
SAIBA+ Veja as diferenças entre a velocidade da luz e a velocidade do som
Fundamentos iniciais
Definição
Lançamento vertical é um termo usado na Física para descrever o movimento de um objeto que é projetado diretamente no ar. O movimento do objeto é afetado pela gravidade, o que faz com que ele desacelere enquanto se move para cima e acelere quando se move para baixo. O movimento do objeto também é afetado pela resistência do ar, que pode fazer com que ele desacelere ainda mais conforme se move para cima e acelere menos quando se move para baixo.
continua após a publicidade
Equações
O movimento de um objeto em lançamento vertical pode ser descrito usando várias equações diferentes. Uma das equações mais básicas é:
![]()
Onde:
- v é a velocidade do objeto no tempo t
- v 0 é a velocidade inicial do objeto
- g é a aceleração da gravidade (aproximadamente 9,8 m/s 2 )
- t é o tempo desde que o objeto foi lançado
Outra equação importante para o lançamento vertical é:
![]()
Onde:
- y é a altura do objeto no tempo t
- y 0 é a altura inicial do objeto
- v 0 é a velocidade inicial do objeto
- g é a aceleração da gravidade (aproximadamente 9,8 m/s 2 )
- t é o tempo desde que o objeto foi lançado
Estas equações podem ser usadas para calcular várias propriedades de um objeto em lançamento vertical, como sua altura máxima e seu tempo de voo.
SAIBA+ Entenda o que é calor Latente e como ele influencia nos materiais.
Exemplos
Lançamento vertical é um conceito fundamental da física que descreve o movimento de um objeto quando ele é lançado diretamente no ar. Vamos explorar dois exemplos de lançamento vertical: movimento de queda livre e movimento vertical para cima.

Movimento de queda livre
O movimento de queda livre é um tipo de lançamento vertical em que um objeto é solto de uma altura e cai direto em direção ao solo. Esse tipo de movimento é regido pelas leis da gravidade e pode ser descrito usando algumas equações-chave. Por exemplo, a distância que um objeto cai durante o movimento de queda livre pode ser calculada usando a equação
![]()
- d é a distância,
- g é a aceleração devido à gravidade
- t é o tempo decorrido.
continua após a publicidade
Outra equação importante para o movimento de queda livre é a equação da velocidade, que descreve como a velocidade do objeto muda ao longo do tempo.
A equação da velocidade para o movimento de queda livre é v = gt, onde v é a velocidade e t é o tempo decorrido. Esta equação mostra que a velocidade de um objeto em movimento de queda livre aumenta linearmente com o tempo.
Lançamento vertical para cima

O lançamento vertical para cima é um tipo de movimento em que um objeto é lançado verticalmente em direção ao topo e depois cai de volta ao solo.
Durante a subida, a velocidade vertical do objeto diminui devido à aceleração da gravidade, até que a velocidade se torna zero no ponto mais alto da trajetória. Durante a queda, a velocidade vertical aumenta devido à aceleração da gravidade, até que o objeto atinge o solo novamente.
Durante o movimento de lançamento vertical para cima, podemos usar as seguintes equações:
- Equação da posição vertical:
![Rendered by QuickLaTeX.com \[y(t) = y_{0} + v_{0}t - \frac{1}{2}gt^{2}\]](https://fisicacuriosa.com/wp-content/ql-cache/quicklatex.com-c7791d509d8ce1caf3e5ccde0c5dcf65_l3.png)
- Equação da velocidade vertical:
![Rendered by QuickLaTeX.com \[v(t) = v_{0} - gt\]](https://fisicacuriosa.com/wp-content/ql-cache/quicklatex.com-7faeddba27228fb16732d0d7a2164233_l3.png)
- Equação da altura máxima:
![Rendered by QuickLaTeX.com \[hmax = y0 +\frac{v0^{2}}{2g}\]](https://fisicacuriosa.com/wp-content/ql-cache/quicklatex.com-8c6e3e87b19a146a89b2013513be9cbe_l3.png)
- Equação do tempo de subida:
![Rendered by QuickLaTeX.com \[tu = \frac{vo}{g}\]](https://fisicacuriosa.com/wp-content/ql-cache/quicklatex.com-efcdfa39e21f89d58bf1274af953e0f1_l3.png)
- Equação do tempo de queda:
![Rendered by QuickLaTeX.com \[ts = \sqrt{\frac{2h}{g}}\]](https://fisicacuriosa.com/wp-content/ql-cache/quicklatex.com-83fbff36d140cb927be81571097de589_l3.png)
- Equação do tempo total de voo:
![Rendered by QuickLaTeX.com \[tv= 2tu\]](https://fisicacuriosa.com/wp-content/ql-cache/quicklatex.com-56fa580365357fbecf824e7fdebda334_l3.png)
Onde:
 é a posição vertical em relação ao ponto de referência (geralmente o solo) no tempo
é a posição vertical em relação ao ponto de referência (geralmente o solo) no tempo 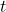 ;
; é a posição inicial vertical;
é a posição inicial vertical; é a velocidade inicial vertical;
é a velocidade inicial vertical;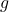 é a aceleração devido à gravidade (aproximadamente 9,81 m/s²);
é a aceleração devido à gravidade (aproximadamente 9,81 m/s²); é a altura máxima atingida pelo objeto;
é a altura máxima atingida pelo objeto; é o tempo de subida (tempo necessário para o objeto alcançar a altura máxima);
é o tempo de subida (tempo necessário para o objeto alcançar a altura máxima);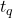 é o tempo de queda (tempo necessário para o objeto cair do ponto mais alto até o solo);
é o tempo de queda (tempo necessário para o objeto cair do ponto mais alto até o solo); é o tempo total de voo (tempo necessário para o objeto ir do solo ao ponto mais alto e depois voltar ao solo).
é o tempo total de voo (tempo necessário para o objeto ir do solo ao ponto mais alto e depois voltar ao solo).
Durante a subida, a velocidade vertical é positiva, enquanto que durante a queda, a velocidade vertical é negativa. No ponto mais alto da trajetória, a velocidade vertical é zero.
SAIBA+ Entenda o que são ondas transversais, longitudinais e mistas
Exercícios
1)Um objeto é solto de uma altura de 50 metros. Qual é o tempo necessário para que o objeto atinja o solo? Considere a aceleração devida à gravidade como 9,81 m/s².
Para resolver esse exercício, podemos utilizar a equação da posição vertical durante a queda livre:
![]()
Sabemos que o objeto foi solto de uma altura de 50 metros (![]() m) e que a velocidade inicial é zero (
m) e que a velocidade inicial é zero (![]() m/s). A aceleração é devida à gravidade, que é constante e igual a 9,81 m/s². Como queremos saber o tempo necessário para que o objeto atinja o solo (
m/s). A aceleração é devida à gravidade, que é constante e igual a 9,81 m/s². Como queremos saber o tempo necessário para que o objeto atinja o solo (![]() m), podemos reescrever a equação acima como:
m), podemos reescrever a equação acima como:
![]()
Simplificando essa equação, temos:
![]()
Isolando o tempo ![]() , temos:
, temos:
![]()
Portanto, o tempo necessário para que o objeto atinja o solo é de aproximadamente 3,19 segundos.
2)Um objeto é lançado verticalmente para cima com uma velocidade inicial de 20 m/s. Qual é a altura máxima que o objeto atinge? Considere a aceleração devida à gravidade como 9,81 m/s².
Para resolver esse exercício, podemos utilizar a equação da altura máxima do lançamento vertical para cima:
![]()
Sabemos que o objeto foi lançado verticalmente para cima, o que significa que sua posição inicial é ![]() m. A velocidade inicial é
m. A velocidade inicial é ![]() m/s e a aceleração devida à gravidade é
m/s e a aceleração devida à gravidade é ![]() m/s². Substituindo esses valores na equação acima, temos:
m/s². Substituindo esses valores na equação acima, temos:
![]()
Portanto, a altura máxima que o objeto atinge é de aproximadamente 20,4 metros.
Para referências de estudo clique aqui