Dilatação Térmica dos sólidos – Fisica Curiosa 2024

Índice

Você conhece o fenômeno físico da dilatação e contração térmica?

Você já parou para pensar o que acontece com os objetos quando são expostos a diferentes temperaturas ou por que alguns materiais se expandem enquanto outros contraem?

Por – Redação do Física Curiosa

A dilatação térmica é um fenômeno que ocorre em praticamente todos os materiais que conhecemos, sejam eles sólidos, líquidos ou gasosos. É um processo intrínseco que envolve mudanças dimensionais em resposta às variações de temperatura.

Essa propriedade pode ser encontrada em nosso cotidiano, desde a simples expansão dos trilhos de trem até a fabricação de termômetros precisos.

Em termos gerais, quando a temperatura de um corpo aumenta, suas dimensões também tendem a aumentar. Esse fenômeno é conhecido como dilatação térmica. Por outro lado, quando a temperatura diminui, é esperado que as dimensões do corpo se contraiam, o que é denominado contração térmica.

SAIBA + entenda como funciona a Física do olho humano.

continua após a publicidade

Explicando a Dilatação térmica

A intensidade das forças intermoleculares, representada por $\vec F$ , varia em função da distância entre as moléculas, representada por $\vec d$ . Quando um corpo é aquecido, as moléculas passam a se mover de forma mais vigorosa, o que implica em um aumento da agitação térmica.

Nesse movimento mais intenso, as moléculas conseguem afastar-se mais umas das outras e, ao mesmo tempo, aproximar-se mais. No entanto, a variação na intensidade das forças intermoleculares não se compensa de forma a não alterar as dimensões do corpo.

continua após a publicidade

Quando as moléculas se aproximam, a intensidade das forças intermoleculares aumenta, e quando se afastam, a intensidade das forças diminui. Portanto, o aumento da agitação térmica leva a uma média de distância entre as moléculas que é maior em comparação com o estado em que o corpo estava em temperatura mais baixa.

Essa alteração na distância média entre as moléculas resulta em uma expansão do corpo quando é aquecido. É por isso que, ao aquecermos um objeto, como um metal, ele geralmente se dilata, aumentando suas dimensões. Esse fenômeno é explicado pelas mudanças nas forças intermoleculares causadas pelo aumento da agitação térmica das moléculas.

+ SAIBA Entenda o que é a temperatura

Dilatação linear dos sólidos

A dilatação térmica dos sólidos é um fenômeno físico interessante e relevante, que ocorre quando um objeto sólido se expande ou contrai devido a variações de temperatura.

Vamos considerar o estudo da dilatação linear dos sólidos, onde nos concentramos na variação do comprimento de um objeto sólido em relação à temperatura.

continua após a publicidade

Imaginemos um fio metálico de comprimento inicial $L_0$ quando está em uma temperatura de referência $\theta_0$ . Se aquecermos esse fio até uma temperatura $\theta$ (onde $\theta$ > $\theta_0$ ), podemos observar que seu comprimento passa a ser L (sendo L > $L_0$ ). Agora, vamos explorar essa relação entre a variação de temperatura e a variação de comprimento.

Para entendermos a dilatação linear, é fundamental reconhecer que o fio metálico é homogêneo, ou seja, possui a mesma composição e propriedades ao longo de sua extensão.

Isso significa que cada unidade de comprimento do fio deve sofrer a mesma dilatação por unidade de variação de temperatura. Em outras palavras, todos os “centímetros” do fio devem sofrer o mesmo aumento de comprimento quando aquecidos igualmente.

Essa propriedade permite que possamos relacionar a variação de comprimento ( $\Delta L$ ) do fio com a variação de temperatura ( $\Delta \theta$ ) que ele sofre.

continua após a publicidade

Para isso, utilizamos uma grandeza chamada coeficiente de dilatação linear ( $\alpha$ ), que é específico para cada material e expressa o quanto o comprimento de um objeto muda para cada variação de temperatura de 1 grau Celsius (ou Kelvin).

Podemos então escrever a relação:

$\begin{equation*} \Delta L = L_0 \cdot \alpha \cdot \Delta \theta \end{equation*}$

Onde $\Delta L$ representa a variação de comprimento do fio, $\alpha$ é o coeficiente de dilatação linear do material, $L_0$ é o comprimento inicial do fio e $\Delta \theta$ é a variação de temperatura experimentada.

É importante ressaltar que a dilatação linear ocorre tanto para o aumento quanto para a diminuição da temperatura. Quando um objeto sólido é resfriado, ele tende a contrair e seu comprimento diminui de acordo com a mesma relação descrita acima.

O coeficiente de dilatação linear α é uma característica intrínseca de cada material e pode ser determinado experimentalmente. Diferentes materiais possuem diferentes coeficientes de dilatação linear, o que significa que a mesma variação de temperatura pode resultar em variações de comprimento distintas em diferentes materiais.

$\begin{equation*} \alpha = \frac{{\Delta L}}{{L_0 \cdot \Delta \theta}} \end{equation*}$

coeficientes de dilatação — Tabela de Coeficientes de Dilatação Linear de Materiais

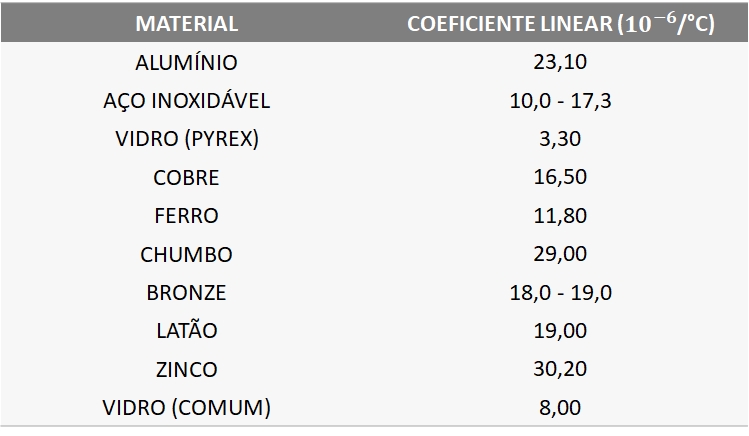
É importante observar que o coeficiente de dilatação linear médio é uma propriedade específica de uma substância e indica a variação média de comprimento por unidade de comprimento quando ocorre uma variação unitária na temperatura. Lembrando que $\Delta L = L - L_0$ , podemos obter a expressão de $L$ em função de $\Delta \theta$ .

$\begin{equation*} \Delta L = L_0 \cdot \alpha \cdot \Delta \theta \end{equation*}$

$\begin{equation*} L - L_0 = L_0 \cdot \alpha \cdot \Delta \theta \end{equation*}$

$\begin{equation*} L = L_0 + L_0 \cdot \alpha \cdot \Delta \theta \end{equation*}$

$\begin{equation*} L = L_0 (1 + \alpha \cdot \Delta \theta) \end{equation*}$

A representação gráfica do comprimento L em função da temperatura $\theta$ está apresentada abaixo:

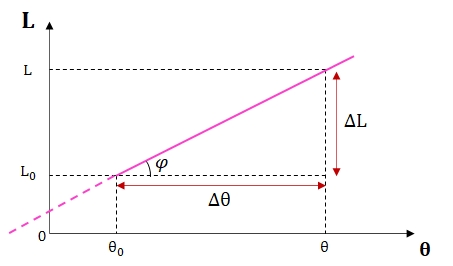
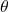continua após a publicidade

Dilatação Superficial dos sólidos

Para simplificar o estudo da dilatação superficial dos sólidos, vamos considerar uma placa metálica de formato quadrado, com lado $L_0$ , que está inicialmente à temperatura $\theta_0$ e é feita de um material com coeficiente de dilatação linear $\alpha$ .

Ao aquecermos a placa até uma temperatura $\theta$ maior que $\theta_0$ , ocorrerá um aumento nas dimensões lineares da placa, resultando em um aumento na área de sua superfície. No entanto, mesmo com esse aumento, a placa continua mantendo a sua forma quadrada.

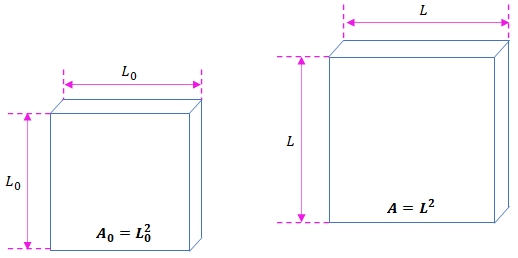
No início, a área da placa é expressa por:

(1) $\begin{equation*} A_0^2 = L_0 ^2 \end{equation*}$

Após o aquecimento, a área da placa foi modificada para:

(2) $\begin{equation*} A^2 = L ^2 \end{equation*}$

Mas podemos relacionar $L$ e $L_0$ através da equação:

$\begin{equation*} L = L_0 (1 + \alpha \cdot \Delta \theta) \end{equation*}$

Elevando ao quadrado ambos os membros da equação, temos:

(3) $\begin{equation*} L^2 = L_0^2 (1 + \alpha \cdot \Delta \theta)^2 \end{equation*}$

Substituindo (I) e (II) em (III), obtemos:

$\begin{equation*} A = A_0 (1 + \alpha \cdot \Delta \theta)^2 \end{equation*}$

$\begin{equation*} A = A_0 (1 + 2\alpha \cdot \Delta \theta + \alpha ^2 \cdot \Delta \theta^2) \end{equation*}$

Como $\alpha$ é da ordem de $10^{-5}$ o termo $\alpha ^2 \cdot \Delta \theta^2$ pode ser desconsiderado devido a ser um valor muito baixo, portanto:

$\begin{equation*} A = A_0 (1 + 2\alpha \cdot \Delta \theta) \end{equation*}$

Ao considerarmos $\beta$ = $2\alpha$ , então:

$\begin{equation*} A = A_0 (1 + \beta \cdot \Delta \theta) \Rightarrow \Delta A = A_0 \beta \cdot \Delta \cdot \theta \end{equation*}$

A equação mencionada pode ser usada para calcular a dilatação superficial em superfícies de diferentes formas, incluindo retangulares, circulares ou de qualquer outra forma.

continua após a publicidade

Ao determinar comprimentos, larguras, áreas ou volumes de buracos, podemos aplicar as equações da dilatação e considerar o coeficiente de dilatação do material do corpo que forma o buraco. A dilatação superficial é calculada multiplicando o coeficiente de dilatação linear pelo comprimento ou raio da superfície e pelo aumento de temperatura.

+ SAIBA saiba o que são escalas termométricas

Aplicações da Dilatação Térmica: Onde utilizamos a Dilatação Térmica na prática

A variação dimensional em resposta a mudanças de temperatura é importante em engenharia e indústria. Essa resposta térmica dos materiais garante o funcionamento adequado e a integridade de sistemas e estruturas. Aqui estão algumas aplicações práticas desse fenômeno:

Construção de Estruturas: Ao projetar e construir estruturas, como pontes e edifícios, a variação dimensional devido às mudanças de temperatura é levada em consideração. Os materiais utilizados nessas estruturas, como concreto, aço e vidro, sofrem expansão ou contração térmica. O conhecimento dessa variação dimensional é essencial para garantir a estabilidade e evitar danos decorrentes das tensões térmicas.
Setor Automotivo: Na indústria automotiva, a variação dimensional é considerada em diferentes componentes e sistemas. Por exemplo, ao projetar o sistema de escape de um veículo, é necessário levar em conta a dilatação térmica dos materiais para evitar vazamentos e garantir a vedação adequada. O mesmo se aplica a outros componentes, como o sistema de arrefecimento e os freios.
Indústria Aeroespacial: Na indústria aeroespacial, onde as temperaturas podem variar drasticamente, a variação dimensional é uma consideração crítica. Os materiais utilizados nas aeronaves, como alumínio, titânio e compósitos, têm coeficientes de expansão térmica diferentes. Portanto, é necessário projetar e selecionar materiais de acordo com as condições de temperatura esperadas para garantir o desempenho adequado e a segurança das aeronaves.

continua após a publicidade

Sistemas de Tubulação: Em sistemas de tubulação, como redes de água, vapor e óleo, a variação dimensional é um fator importante a ser considerado. Os tubos e conexões utilizados nesses sistemas podem sofrer dilatação ou contração térmica, o que pode levar a tensões e deformações. Juntas de expansão e dispositivos de compensação são utilizados para acomodar essas variações dimensionais e evitar danos nas tubulações.
Indústria Eletrônica: Na indústria eletrônica, a variação dimensional é relevante em componentes como circuitos impressos e semicondutores. As mudanças de temperatura podem afetar o desempenho e a confiabilidade desses componentes. O conhecimento da variação dimensional ajuda a projetar dispositivos eletrônicos mais robustos, levando em consideração os efeitos térmicos.

Esses são apenas alguns exemplos das muitas aplicações práticas da variação dimensional em resposta às mudanças de temperatura. O entendimento desse fenômeno é essencial para projetar estruturas, sistemas e componentes confiáveis e duráveis, levando em consideração as características térmicas dos materiais envolvidos.

Referências:

Tópicos de Física – Volume 2

Curso de Física Básica: Fluidos, Oscilações e Ondas, Calor (Volume 2)