Você conhece a espiral de Fibonacci?
A Espiral de Fibonacci é uma fascinante manifestação da sequência numérica que leva o nome do matemático italiano do século XIII, Leonardo Fibonacci. A sequência de Fibonacci é gerada adicionando os dois números anteriores para obter o próximo número na sequência: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 e assim por diante. Essa sequência tem aplicações em várias áreas, desde a matemática pura até a biologia, arte e arquitetura.
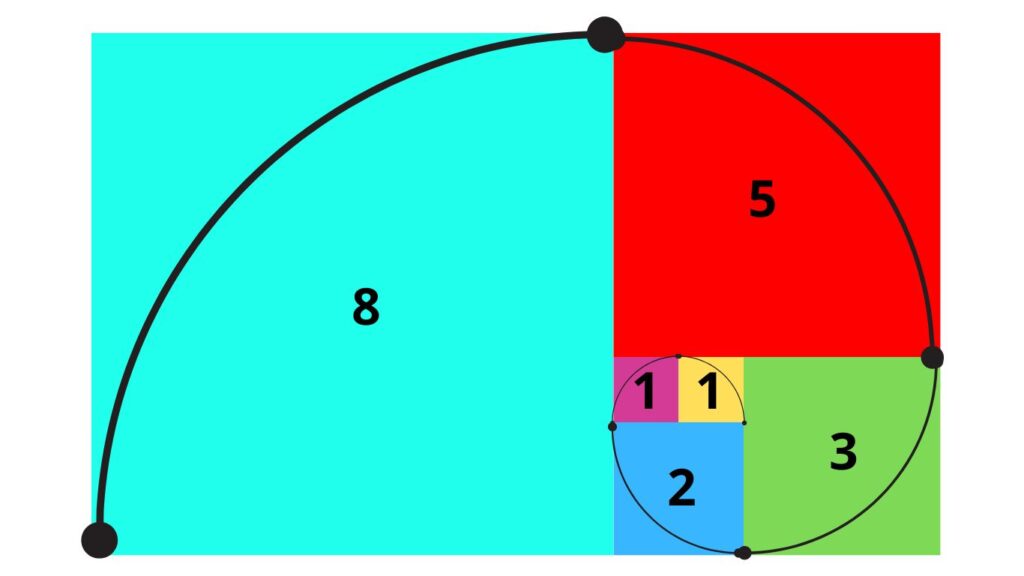
Uma das representações mais intrigantes dessa sequência é a Espiral de Fibonacci, na qual quadrados de tamanhos proporcionais aos números da sequência são desenhados e conectados em uma espiral contínua. Esta espiral é caracterizada por uma notável regularidade e beleza, encontrada em muitos fenômenos naturais e obras de arte.
Sequencia de Fibonacci: origens e natureza
A Espiral de Fibonacci tem suas raízes na natureza. Muitas estruturas naturais exibem uma proporção que se alinha com a sequência de, um fenômeno conhecido como a proporção áurea ou divina. Por exemplo, a disposição das sementes em um girassol, as espirais de uma concha de caracol, os galhos de uma árvore e até mesmo a disposição das escamas em um cone de pinha seguem a sequência de Fibonacci.
Essa conexão com a natureza despertou o interesse de cientistas, artistas e filósofos ao longo dos séculos, levando a investigações mais aprofundadas sobre as implicações matemáticas e estéticas da sequência e da Espiral de Fibonacci.
continua após a publicidade
Matemática por Trás da Beleza
A beleza da Espiral está profundamente enraizada em sua estrutura matemática simples, mas elegantemente complexa. A cada iteração da espiral, a proporção entre os lados dos quadrados adjacentes se aproxima da proporção áurea, aproximadamente 1,61803398875, uma constante matemática representada pela letra grega phi (φ). Esta proporção é considerada esteticamente agradável e é frequentemente encontrada em obras de arte e arquitetura ao longo da história.
Além disso, a Espiral exibe propriedades geométricas intrigantes, como o fato de que a largura de cada quadrado é igual à soma dos dois quadrados anteriores. Essa propriedade está intimamente ligada à definição da sequência de Fibonacci e fornece uma explicação clara para a formação da espiral.
Aplicações e Implicações
Além de sua beleza estética e interesse matemático, a Espiral tem várias aplicações práticas em diversas áreas. Na arte e no design, a espiral é frequentemente usada para criar composições visualmente atraentes e equilibradas. Na arquitetura, a proporção áurea é muitas vezes empregada para criar estruturas que são percebidas como esteticamente agradáveis.
Além disso, a compreensão dela é crucial em campos como a biologia, onde padrões naturais baseados nessa sequência são observados em várias estruturas vivas, desde a disposição de folhas em uma planta até a estrutura de proteínas em um organismo.
Aqui estão alguns exemplos de onde podemos encontrar esta sequência na natureza:
- Flores e Plantas: A disposição das folhas em muitas plantas segue um padrão baseado na sequência de Fibonacci. Por exemplo, em muitas plantas, como girassóis e alcachofras, as folhas são arranjadas em espirais que seguem a sequência de Fibonacci. Além disso, o número de pétalas em muitas flores também segue a sequência de Fibonacci, como é o caso dos lírios, margaridas e muitas outras.
- Frutas e Vegetais: Muitas frutas e vegetais exibem uma disposição baseada na sequência de Fibonacci. Por exemplo, as sementes em um girassol ou abacaxi geralmente seguem padrões de espiral que correspondem à sequência de Fibonacci. Da mesma forma, a disposição de espirais em uma pinha ou no fundo de uma maçã é frequentemente baseada nessa sequência.
- Animais Marinhos: Conchas de caracol e conchas de moluscos muitas vezes exibem padrões de espiral que seguem a sequência de Fibonacci. Além disso, algumas criaturas marinhas, como estrelas do mar e ouriços-do-mar, têm um número de braços que segue a sequência de Fibonacci.
- Animais Terrestres: Os padrões de espiral da pele de alguns animais, como lesmas e caramujos, muitas vezes seguem a sequência. Além disso, algumas estruturas anatômicas, como a proporção entre os ossos de uma mão humana, também exibem proporções próximas à proporção áurea.
- Formações Naturais: A forma como as nuvens se formam e se movem muitas vezes segue padrões que refletem a sequência de Fibonacci. Além disso, a estrutura de muitas galáxias em espiral e a disposição dos braços em uma galáxia espiral também podem ser modeladas com base nessa sequência.
A Espiral de Fibonacci é muito mais do que uma curiosidade matemática; é um símbolo da harmonia entre a matemática, a natureza e a estética. Sua presença onipresente na natureza e sua aplicação em diversos campos do conhecimento destacam sua importância e relevância. Ao explorar esse fenômeno, somos lembrados da beleza e da complexidade subjacentes ao mundo natural e à matemática que o descreve.
Gostou? Compartilhe =)